El Teorema de Stokes es una herramienta fundamental en el campo del cálculo vectorial y la física. Este teorema establece una relación entre el flujo de un campo vectorial a través de una superficie cerrada y la circulación del campo a lo largo de la frontera de dicha superficie. En otras palabras, nos permite calcular la circulación de un campo vectorial en una región cerrada a partir del flujo a través de una superficie que encierra dicha región.
Este teorema fue formulado por el matemático y físico británico George Gabriel Stokes en el siglo XIX, y desde entonces ha sido ampliamente utilizado en diversas ramas de la ciencia y la ingeniería. Su importancia radica en que nos permite relacionar dos conceptos fundamentales en el estudio de los campos vectoriales: el flujo y la circulación.
Fórmula de Torricelli
La fórmula de Torricelli es una ecuación fundamental en la física que relaciona la velocidad de un fluido en un orificio con la altura del fluido sobre el orificio. Esta fórmula fue descubierta por el científico italiano Evangelista Torricelli en el siglo XVII y es una consecuencia directa del principio de Bernoulli.
La fórmula establece que la velocidad de salida del fluido a través de un orificio es igual a la velocidad que adquiriría un objeto en caída libre desde la altura del fluido sobre el orificio. Matemáticamente, la fórmula se expresa de la siguiente manera:
v = √(2gh)
Donde v es la velocidad de salida del fluido, g es la aceleración debida a la gravedad y h es la altura del fluido sobre el orificio. Esta fórmula es de gran utilidad en la hidrodinámica y se aplica en diversos campos como la ingeniería civil, la hidrología y la meteorología.
Introducción al magnetismo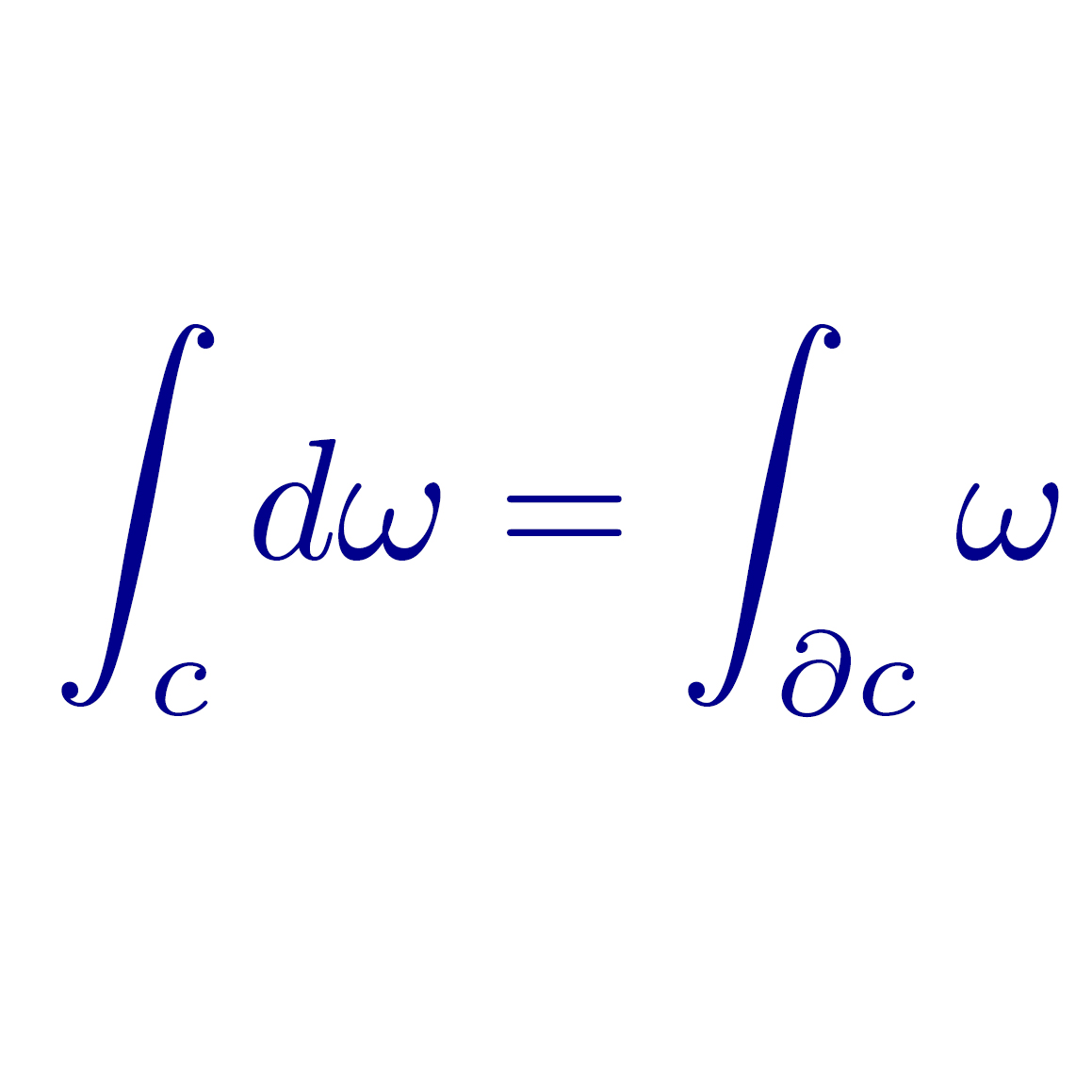
El magnetismo es una fuerza fundamental de la naturaleza que ha fascinado a los científicos y a las personas durante siglos. Es la fuerza que permite que los imanes atraigan o repelan objetos metálicos y también está presente en fenómenos como la electricidad y el electromagnetismo.
El magnetismo se origina en los átomos, que están compuestos por partículas cargadas llamadas electrones. Estos electrones tienen una propiedad llamada espín, que es como una pequeña brújula que puede apuntar hacia arriba o hacia abajo. Cuando los espines de los electrones en un material se alinean en la misma dirección, se crea un campo magnético.
El campo magnético es invisible pero se puede sentir y medir. Los imanes tienen dos polos, el polo norte y el polo sur, y los polos opuestos se atraen mientras que los polos iguales se repelen. Esto se debe a que las líneas de fuerza del campo magnético se mueven desde el polo norte hacia el polo sur.
¿Qué es el magnetismo?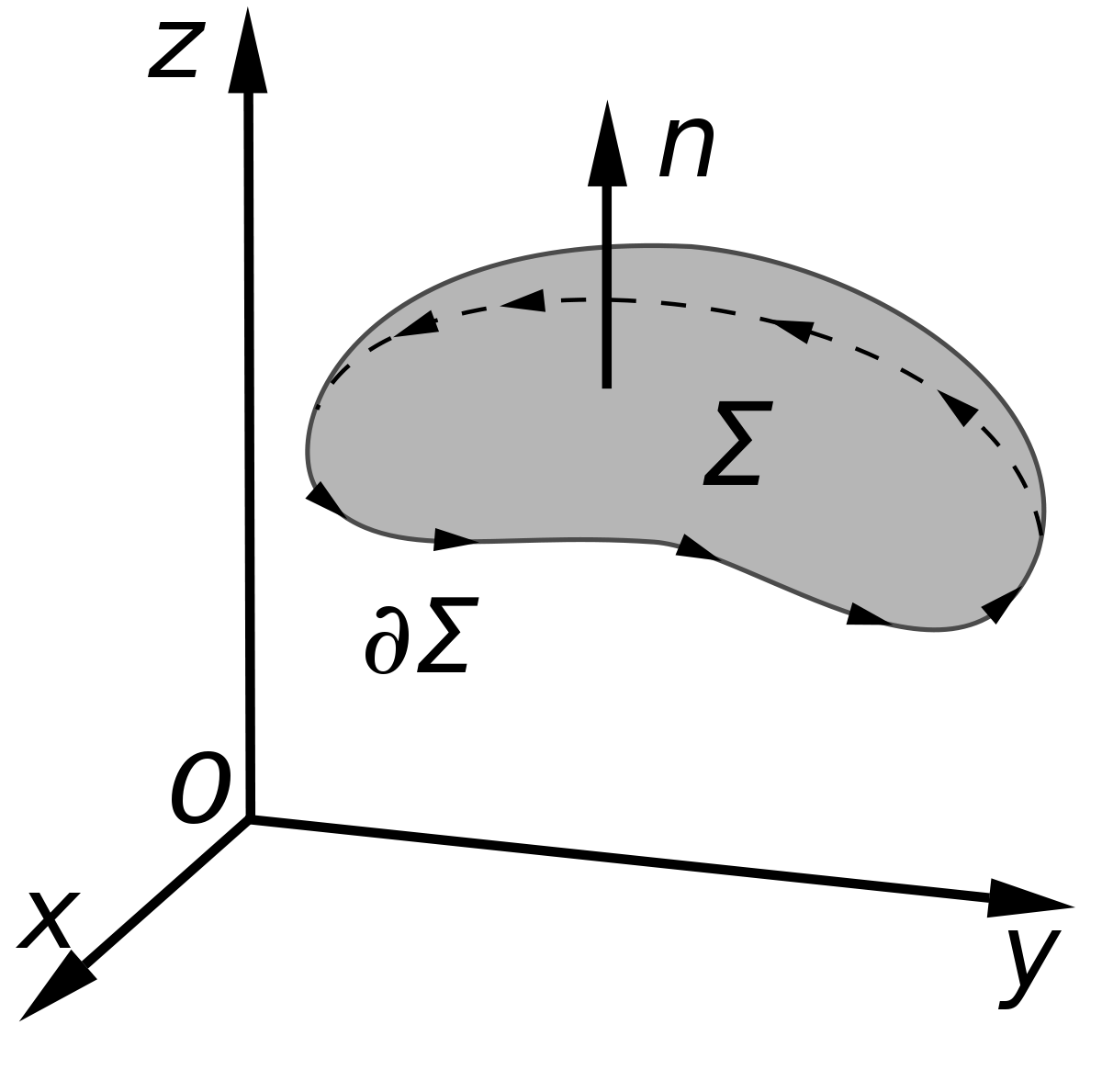
El magnetismo es una fuerza natural que se produce entre los objetos que tienen propiedades magnéticas. Estas propiedades magnéticas se deben a la presencia de campos magnéticos, que son generados por la presencia de cargas eléctricas en movimiento. El magnetismo es una de las fuerzas fundamentales de la naturaleza y desempeña un papel importante en muchos aspectos de nuestra vida cotidiana.
Los imanes son objetos que tienen propiedades magnéticas y pueden atraer o repeler otros objetos magnéticos. Los imanes tienen dos polos, el polo norte y el polo sur, que interactúan entre sí. Cuando dos polos opuestos se acercan, se atraen, mientras que cuando dos polos iguales se acercan, se repelen. Esta interacción magnética es lo que permite que los imanes se adhieran a superficies metálicas o que se atraigan entre sí.
El magnetismo también está presente en la Tierra, donde se manifiesta en forma de un campo magnético terrestre. Este campo magnético es generado por el movimiento de hierro líquido en el núcleo de la Tierra. El campo magnético terrestre es lo que permite que las brújulas funcionen, ya que las agujas de las brújulas se alinean con el campo magnético y apuntan hacia el polo norte magnético.
Propiedades magnéticas
El magnetismo es una propiedad fundamental de ciertos materiales que les permite atraer o repeler otros objetos. Esta propiedad se debe a la existencia de campos magnéticos, que son generados por la presencia de corriente eléctrica o por el movimiento de partículas cargadas. Los imanes son objetos que tienen la capacidad de generar campos magnéticos de forma natural.
Existen diferentes propiedades magnéticas que caracterizan a los materiales. Una de ellas es la magnetización, que es la capacidad de un material para alinearse con un campo magnético externo y convertirse en un imán temporal. Otro concepto importante es la permeabilidad magnética, que indica la facilidad con la que un material puede ser magnetizado. Los materiales ferromagnéticos, como el hierro y el níquel, tienen una alta permeabilidad magnética y son muy utilizados en la fabricación de imanes.
El magnetismo también está relacionado con el flujo magnético, que es una medida de la cantidad de campo magnético que atraviesa una superficie. El flujo magnético se representa mediante líneas de campo, que son líneas imaginarias que indican la dirección y la intensidad del campo magnético. El Teorema de Stokes es una herramienta matemática que permite calcular el flujo magnético a través de una superficie cerrada a partir del campo magnético en su borde. Este teorema es fundamental en el estudio del magnetismo y tiene aplicaciones en diversas áreas de la física y la ingeniería.
Campos magnéticos
Los campos magnéticos son regiones del espacio donde se ejerce una fuerza magnética sobre las partículas cargadas en movimiento. Estos campos son generados por corrientes eléctricas y por el movimiento de partículas cargadas, como electrones. El magnetismo es una propiedad fundamental de la materia y está presente en diversos fenómenos naturales.
Los campos magnéticos se representan mediante líneas de campo, que indican la dirección y la intensidad del campo en cada punto. Estas líneas forman circuitos cerrados, lo que significa que no hay fuentes ni sumideros de campo magnético. Además, los campos magnéticos son siempre perpendiculares a la dirección del movimiento de las partículas cargadas.
El estudio de los campos magnéticos es fundamental para entender fenómenos como la atracción y repulsión entre imanes, la generación de electricidad en generadores y transformadores, y el funcionamiento de dispositivos electrónicos como motores y altavoces. Además, los campos magnéticos también tienen aplicaciones en medicina, como en la resonancia magnética.
Flujo magnético
El flujo magnético es una medida de la cantidad de líneas de campo magnético que atraviesan una superficie determinada. Se representa por el símbolo Φ y se mide en Weber (Wb). El flujo magnético está relacionado con la intensidad del campo magnético y el área de la superficie a través de la cual pasa el campo.
El Teorema de Stokes es una herramienta matemática que nos permite calcular el flujo magnético a través de una superficie cerrada. Este teorema establece que el flujo magnético a través de una superficie cerrada es igual a la integral del rotacional del campo magnético sobre la superficie.
En otras palabras, el Teorema de Stokes nos permite relacionar el flujo magnético con las propiedades del campo magnético en una región determinada. Esto es especialmente útil en situaciones donde el campo magnético no es uniforme o varía en el tiempo.
Definición de flujo magnético
El flujo magnético es una medida de la cantidad de líneas de campo magnético que atraviesan una superficie determinada. Se puede pensar en el flujo magnético como el número de líneas de campo que atraviesan una superficie en particular. Cuanto mayor sea el número de líneas de campo que atraviesan la superficie, mayor será el flujo magnético.
El flujo magnético se representa mediante el símbolo Φ y se mide en Weber (Wb). Es importante tener en cuenta que el flujo magnético solo se produce cuando hay un campo magnético presente y una superficie que atraviesa ese campo. Si no hay campo magnético o si la superficie no atraviesa el campo, el flujo magnético será cero.
El Teorema de Stokes es una herramienta matemática que nos permite calcular el flujo magnético a través de una superficie cerrada utilizando la circulación del campo magnético alrededor de la frontera de la superficie. Este teorema es una consecuencia directa de las ecuaciones de Maxwell y es fundamental en el estudio del magnetismo y el electromagnetismo.
Unidades de medida del flujo magnético
El flujo magnético es una medida de la cantidad de campo magnético que atraviesa una superficie determinada. Se representa con el símbolo Φ y se mide en Weber (Wb) en el Sistema Internacional de Unidades (SI).
El Weber es una unidad bastante grande, por lo que también se utiliza el mil Weber (mWb) como submúltiplo. Además, existen otras unidades de medida del flujo magnético, como el Maxwell (Mx) en el sistema CGS (Centímetro-Gramo-Segundo) y el Tesla Metro Cuadrado (T·m²) en el sistema MKS (Metro-Kilogramo-Segundo).
Estas unidades son importantes para calcular el flujo magnético a través de una superficie y entender cómo se relaciona con el campo magnético y las corrientes eléctricas. El Teorema de Stokes nos permite calcular el flujo magnético a través de una curva cerrada utilizando la integral de línea del campo magnético.
Flujo magnético a través de una superficie
El flujo magnético a través de una superficie es una medida de la cantidad de líneas de campo magnético que atraviesan dicha superficie. Se puede calcular utilizando el Teorema de Stokes, que establece una relación entre el flujo magnético y la circulación del campo magnético alrededor de la frontera de la superficie.
El Teorema de Stokes establece que el flujo magnético a través de una superficie cerrada es igual a la circulación del campo magnético alrededor de la frontera de la superficie. Esto significa que si trazamos una línea cerrada alrededor de la superficie y calculamos la circulación del campo magnético a lo largo de esa línea, obtendremos el mismo valor que si calculamos el flujo magnético a través de la superficie.
El flujo magnético se expresa en unidades de Weber (Wb) y se calcula multiplicando el campo magnético por el área de la superficie y el coseno del ángulo entre el campo magnético y la normal a la superficie. Cuanto mayor sea el campo magnético o el área de la superficie, mayor será el flujo magnético.
En resumen, el flujo magnético a través de una superficie se calcula utilizando el Teorema de Stokes y es una medida de la cantidad de líneas de campo magnético que atraviesan dicha superficie. Es importante tener en cuenta el campo magnético, el área de la superficie y el ángulo entre el campo magnético y la normal a la superficie para obtener un valor preciso del flujo magnético.
El Teorema de Stokes
El Teorema de Stokes es un concepto fundamental en el campo del cálculo vectorial y la física. Este teorema establece una relación entre el flujo de un campo vectorial a través de una superficie cerrada y la circulación de ese campo a lo largo de la frontera de la superficie. En otras palabras, el teorema describe cómo el flujo y la circulación de un campo vectorial están relacionados entre sí.
Para entender mejor el Teorema de Stokes, es importante comprender algunos conceptos clave. En primer lugar, un campo vectorial es una función que asigna un vector a cada punto en el espacio. Por ejemplo, el campo de velocidades de un fluido en movimiento es un campo vectorial. El flujo de un campo vectorial a través de una superficie se refiere a la cantidad de campo que atraviesa la superficie en una dirección específica. Por otro lado, la circulación de un campo vectorial se refiere a la integral de línea del campo a lo largo de una curva cerrada.
El Teorema de Stokes establece que el flujo de un campo vectorial a través de una superficie cerrada es igual a la circulación de ese campo a lo largo de la frontera de la superficie. Esto implica que el flujo y la circulación están intrínsecamente relacionados y dependen uno del otro. El teorema es una generalización del Teorema de Gauss, que relaciona el flujo de un campo vectorial a través de una superficie cerrada con la divergencia de ese campo en el interior de la superficie.
En resumen, el Teorema de Stokes es una herramienta poderosa para analizar el comportamiento de los campos vectoriales en el espacio. Permite relacionar el flujo y la circulación de un campo a través de una superficie cerrada, lo que proporciona información valiosa sobre las propiedades y características del campo en cuestión.
Concepto y aplicaciones
El Teorema de Stokes es una herramienta fundamental en el campo del cálculo vectorial y la física. Este teorema establece una relación entre el flujo de un campo vectorial a través de una superficie cerrada y la circulación de ese campo a lo largo de la frontera de dicha superficie.
En términos más simples, el Teorema de Stokes nos permite calcular la circulación de un campo vectorial alrededor de una curva cerrada a partir del flujo de ese campo a través de una superficie que encierra dicha curva. Esto es especialmente útil en problemas donde se desea determinar la circulación de un campo magnético alrededor de una trayectoria cerrada.
Las aplicaciones del Teorema de Stokes son numerosas y se encuentran en diversos campos de la física y la ingeniería. Por ejemplo, en electromagnetismo, este teorema es utilizado para calcular la fuerza electromotriz inducida en un circuito cerrado por un campo magnético variable. También es utilizado en la mecánica de fluidos para analizar el flujo de un fluido alrededor de una superficie cerrada.
Explicación matemática del Teorema de Stokes
El Teorema de Stokes es un concepto fundamental en el campo del cálculo vectorial que establece una relación entre el flujo de un campo vectorial a través de una superficie cerrada y la circulación del campo a lo largo de la frontera de esa superficie. En términos más simples, el teorema nos permite relacionar el comportamiento de un campo vectorial en una región tridimensional con el comportamiento en su frontera.
Para entender mejor el Teorema de Stokes, es necesario comprender algunos conceptos matemáticos clave. En primer lugar, debemos entender qué es un campo vectorial. Un campo vectorial asigna un vector a cada punto en el espacio, lo que significa que en cada punto hay una magnitud y una dirección asociadas. Por ejemplo, el campo de velocidades en un fluido es un campo vectorial, ya que en cada punto del fluido hay una velocidad y una dirección específicas.
El Teorema de Stokes establece que la circulación de un campo vectorial a lo largo de una curva cerrada es igual al flujo del rotacional del campo a través de cualquier superficie orientada cuya frontera sea esa curva cerrada. En otras palabras, si tenemos un campo vectorial y una superficie cerrada que encierra una región en el espacio, la circulación del campo a lo largo de la frontera de esa superficie es igual al flujo del rotacional del campo a través de la superficie.
Este teorema es extremadamente útil en muchas áreas de la física y la ingeniería, ya que nos permite relacionar fenómenos en el interior de una región con el comportamiento en su frontera. Por ejemplo, en la electromagnetismo, el Teorema de Stokes se utiliza para relacionar el campo magnético alrededor de un circuito cerrado con la corriente eléctrica que atraviesa ese circuito. En resumen, el Teorema de Stokes es una herramienta poderosa que nos permite comprender y analizar el comportamiento de los campos vectoriales en el espacio tridimensional.

